---
theme: gaia
title: Using Formal Methods to Discover a Bug in the Chapel Compiler
backgroundColor: #fff
---
<!-- _class: lead -->
<style>
section {
    font-size: 25px;
}
blockquote {
    padding: 15px;
    background-color: #f0f0ff;
}

div.side-by-side {
    display: flex;
    justify-content: space-between;
    gap: 20px;
}

div.side-by-side > div {
    flex: 1;
}
</style>

# <!--fit--> **Using Formal Methods to Discover a Bug in the Chapel Compiler**
Daniel Fedorin, HPE

---

# Terms

* What are **formal methods**?
    * Techniques rooted in computer science and mathematics to specify and verify systems
* What part of the **Chapel compiler**?
    * The 'Dyno' compiler front-end, particularly its use/import resolution phase.
    * This piece is used by the production Chapel compiler.

---

# The Story

I have a story in three parts.

1. I found it very hard to think through a section of compiler code.
    - Specifically, code that performed lookups in `use`s/`import`s

2. I used the [Alloy Analyzer](https://alloytools.org/) to model the assumptions and behavior of the code.
    - I had little background in Alloy, but some background in (formal) logic

3. This led me to discover a bug in the compiler that I then fixed.
    - Re-creating the bug required some gymnastics that were unlikely to occur in practice.

---

<!-- _class: lead -->
# Background: Chapel's Scope Lookups

---

# The Humble `foo`
Imagine you see the following snippet of Chapel code:

```chapel
foo();
```

Where do you look for `foo`? The answer is quite complicated, and depends
strongly on the context of the call.

Moreover, the order of where to look matters: method calls are preferred
over global functions, "nearer" functions are preferred over "farther" ones.

---

# The Humble `foo` (example 1)

```chapel
module M1 {
  record R {
    proc foo() { writeln("R.foo"); }
  }
  proc foo() { writeln("M1.foo"); }

  foo(); // which 'foo'?
}
```

Here, things are pretty straightforward: we look in scope `M1`. `R.foo` is not
in it, but `M1.foo` is. We return it.

---

# The Humble `foo` (example 2)

```chapel
module M1 {
  record R {}

  proc R.foo() { writeln("R.foo"); }
  proc foo() { writeln("M1.foo"); }

  foo(); // which 'foo'?
}
```

Here, things are bit trickier. Since we are not inside a method, we know
that `foo()` could not be a call to a method. Thus, we rule out `R.foo`,
and find `M1.foo` in `M1`.

---

# The Humble `foo` (example 3)

```chapel
module M1 {
  record R {}

  proc R.foo() { writeln("R.foo"); }
  proc foo() { writeln("M1.foo"); }

  proc R.someMethod() {
    foo(); // which 'foo'?
  }
}
```

* Both `R.foo` and `M1.foo` would be valid candidates.
* We give priority to methods over global functions. So, the compiler would:
    * Search `R` and its scope (`M1`) for methods named `foo`.
    * If that fails, search `M1` for any symbols `foo`.
* We've had to look at `M1` twice! (once for methods, once for non-methods)

---

# The Humble `foo` (example 4)

```chapel
module M1 {
  record R {}

  proc foo() { writeln("R.foo"); }
}
module M2 {
  use M1;

  proc R.someMethod() {
    foo(); // which 'foo'?
  }
}
```

Here, we search the scope of `R` and `M1`, but **only for public symbols**.

---


# How Chapel's Compiler Handles This

We want to:
- Respect the priority order
  - Including preferring methods over non-methods
  - As a result, we search the scopes multiple times
- Avoid any extra work
  - This includes redundant re-searches
  - Example redundant search: looked up "all symbols", then later "all public symbols"

```C++
enum { PUBLIC = 1, NOT_PUBLIC = 2, METHOD_FIELD = 4, NOT_METHOD_FIELD = 8, /* ... */ };
```

1. For each scope, save the flags we've already searched with
2. When searching a scope again, exclude the flags we've already searched with

This was handled by two bitfields: `filter` and `excludeFilter`.

---

# Populating `filter` and `excludeFilter`

```C++
if (skipPrivateVisibilities) { // depends on context of 'foo()'
  filter |= IdAndFlags::PUBLIC;
}

if (onlyMethodsFields) {
  filter |= IdAndFlags::METHOD_FIELD;

} else if (!includeMethods && receiverScopes.empty()) {
  filter |= IdAndFlags::NOT_METHOD;
}
```

```C++
excludeFilter = previousFilter;
```

```C++
// scary!
previousFilter = filter & previousFilter;
```

Code notes `previousFilter` is an approximation.

---
# Possible Problems

* `previousFilter` is an approximation.
    * For `previousFilter = PUBLIC` and `filter = METHOD_FIELD`, we get
      `previousFilter = 0`, indicating no more searches should be done.
    * But we're missing private non-methods!
* However, no case we knew of hit this combination of searches, or any like it.
    * All of our language tests passed.
    * Code seemed to work.
* If only there was a way I could get a computer to check whether such a combination
  could occur...

---

<!-- _class: lead -->
# Formal Methods

---
# Types of Formal Methods

- Model checking involves formally describing the behavior of a system, then having a solver check whether other desired properties hold.
    - Alloy is an example of a model checker.
    - TLA is another famous example.
- Theorem proving is a heavier weight approach that involves building a formal proof of correctness.
    - Coq and Isabelle are examples of theorem provers.
---
<style scoped>
li:nth-child(2) { color: lightgrey; }
</style>
# Types of Formal Methods

- Model checking involves formally describing the behavior of a system, then having a solver check whether other desired properties hold.
    - Alloy is an example of a model checker.
    - TLA is another famous example.
- Theorem proving is a heavier weight approach that involves building a formal proof of correctness.
    - Coq and Isabelle are examples of theorem provers.



**Reason**: I was in the middle of developing compiler code. I wanted to sketch
the assumptions I was making and see if they held up.

---

# A Primer on Logic

Model checkers like Alloy are rooted in temporal logic, which builds on
first-order logic. This includes:

- Variables (e.g. $x$, $y$)
    - These represent any objects in the logical system.
- Predicates (e.g. $P(x)$, $Q(x,y)$)
    - These represent properties of objects, or relationships between objects.
- Logical connectives (e.g. $\land$, $\lor$, $\neg$, $\Rightarrow$)
    - These are used to combine predicates into more complex statements.
    - $\land$ is "and", $\lor$ is "or", $\neg$ is "not", $\Rightarrow$ is "implies".
- Quantifiers (e.g. $\forall$, $\exists$)
    - $\forall x. P(x)$ (in Alloy: `all x { P(x) }`) means "for all $x$, $P(x)$ is true".
    - $\exists x. P(x)$ (in Alloy: `some x { P(x)}`) means "there exists an $x$ such that $P(x)$ is true".

---

# A Primer on Logic (example)

Example statement: "Bob has a son who likes all compilers".

$$
\exists x. (\text{Son}(x, \text{Bob}) \land \forall y. (\text{Compiler}(y) \Rightarrow \text{Likes}(x, y)))
$$

In Alloy:

```alloy
some x { Son[x, Bob] and all y { Compiler[y] implies Likes[x, y] } }
```

---

# A Primer on Temporal Logic

Temporal logic provides additional operators to reason about how properties change over time.

- $\Box p$ (in Alloy: `always p`): A statement that is always true.
- $\Diamond p$ (in Alloy: `eventually p`) : A statement that will be true at some point in the future.

In Alloy specifically, we can mention the next state of a variable using `'`.

```alloy
// pseudocode:
//   the next future value of previousFilter will be the intersection of filter
//   and the current value
previousFilter' = filter & previousFilter;
```

---

# A Primer on Temporal Logic (example)

Some examples:

$$
\Box(\text{like charges repel})
$$
$$
\Diamond(\text{the sun is in the sky})
$$

In Alloy:

```alloy
// likeChargesRepel and theSunIsInTheSky are predicates defined elsewhere

always likeChargesRepel

// good thing it's not `always`
eventually theSunIsInTheSky
```

---

# Search Configuration in Alloy

Instead of duplicating `METHOD` and `NOT_METHOD`, use two sets of flags (the regular and the "not").

```alloy
enum Flag {Method, MethodOrField, Public}

sig Bitfield {
    , positiveFlags: set Flag
    , negativeFlags: set Flag
}

sig FilterState { , curFilter: Bitfield }

```


__Takeaway__: We represent the search flags as a `Bitfield`, which encodes `PUBLIC`, `NOT_PUBLIC`, etc.

---

# Constructing Bitfields

Alloy doesn't allow us to define functions that somehow combine bitfields. We might want to write:

```chapel
proc addFlag(b: Bitfield, flag: Flag): Bitfield {
    return Bitfield(b.positiveFlags + flag, b.negativeFlags);
}
```

Instead, we can _relate_ two bitfields using a predicate.

> This bitfield is like that bitfield, but with this flag added.

```chapel
pred addBitfieldFlag[b1: Bitfield, b2: Bitfield, flag: Flag] {
    b2.positiveFlags = b1.positiveFlags + flag
    b2.negativeFlags = b1.negativeFlags
}
```

---

# Constructing Bitfields

Alloy doesn't allow us to define functions that somehow combine bitfields. We might want to write:

```chapel
proc addFlag(b: Bitfield, flag: Flag): Bitfield {
    return Bitfield(b.positiveFlags + flag, b.negativeFlags);
}
```

Instead, we can _relate_ two bitfields using a predicate.

> This bitfield is exactly like that bitfield.

```chapel
pred bitfieldEqual[b1: Bitfield, b2: Bitfield] {
    b1.positiveFlags = b2.positiveFlags and b1.negativeFlags = b2.negativeFlags
}
```

---

# Modeling Possible Searches

Alloy isn't an imperative language. We can't mutate variables like we do in C++. Instead, we model how each statement changes the state, by relating the "current" state to the "next" state.

<div class="side-by-side">
  <div>

```C++
  filter |= IdAndFlags::PUBLIC;
```

  </div>
  <div>

```alloy
  addBitfieldFlag[filterNow, filterNext, Public]
```

  </div>
</div>

This might remind you of [Hoare Logic](https://en.wikipedia.org/wiki/Hoare_logic), where statements like:

$$
 \{ P \} \; s \; \{ Q \}
$$

Read as:

> If $P$ is true before executing $s$, then $Q$ will be true after executing $s$.

$$
 \{ \text{filter} = \text{filterNow} \} \; \texttt{filter |= PUBLIC} \; \{ \text{filter} = \text{filterNext} \}
$$

---

# Modeling Possible Searches

To combine several statements, we make it so that the "next" state of one statement is the "current" state of the next statement.

<div class="side-by-side">
  <div>

```C++
  curFilter |= IdAndFlags::PUBLIC;
  curFilter |= IdAndFlags::METHOD_FIELD;
```

  </div>
  <div>

```alloy
  addBitfieldFlag[filterNow, filterNext1, Public]
  addBitfieldFlag[filterNext1, filterNext2, Method]
```

  </div>
</div>

This is reminiscent of sequencing Hoare triples:

$$
 \{ P \} \; s_1 \; \{ Q \} \; s_2 \; \{ R \}
$$

---

# Modeling Possible Searches

Finally, if C++ code has conditionals, we need to allow for the possibility of either branch being taken. We do this by using "or" on descriptions of the next state.

<div class="side-by-side">
  <div>

```C++
  if (skipPrivateVisibilities) {
    curFilter |= IdAndFlags::PUBLIC;
  }






  if (onlyMethodsFields) {
    curFilter |= IdAndFlags::METHOD_FIELD;
  } else if (!includeMethods && receiverScopes.empty()) {
    curFilter |= IdAndFlags::NOT_METHOD;
  }


                                                                                  
```
  </div>
  <div>

```alloy
  addBitfieldFlag[initialState.curFilter, bitfieldMiddle, Public] or
  bitfieldEqual[initialState.curFilter, bitfieldMiddle]







  // If it's a method receiver, add method or field restriction
  addBitfieldFlag[bitfieldMiddle, filterState.curFilter, MethodOrField] or

  // if it's not a receiver, filter to non-methods (could be overridden)
  addBitfieldFlagNeg[bitfieldMiddle, filterState.curFilter, Method] or

  // Maybe methods are not being curFilterd but it's not a receiver, so no change.
  bitfieldEqual[bitfieldMiddle, filterState.curFilter]
```
  </div>
</div>

Putting this into a predicate, `possibleState`, we encode what searches the compiler can undertake.

**Takeaway**: We encoded the logic that configures possible searches in Alloy. This instructs the analyzer about possible cases to consider.

---

# Modeling `previousFilter`

So far, all we've done is encoded what queries the compiler might make about a scope.

We still need to encode how we save the flags we've already searched with.

Model the search state with a "global" (really, unique) variable:

```alloy
/* Initially, no search has happeneed for a scope, so its 'previousFilter' is not set to anything. */
one sig NotSet {}

one sig SearchState {
    , var previousFilter: Bitfield + NotSet
}
```

Above, `+` is used for union. `previousFilter` can either be a `Bitfield` or `NotSet`.

---

# Modeling `previousFilter`

If no previous search has happened, we set `previousFilter` to the current `filter`.

Otherwise, we set `previousFilter` to the intersection of `filter` and `previousFilter`, as mentioned before.

<div class="side-by-side">
  <div>

```C++
  if (hasPrevious) {
    previousFilter = filter & previousFilter;
  } else {
    previousFilter = filter;
  }
```

  </div>
  <div>

```alloy
  pred update[toSet: Bitfield + NotSet, setTo: FilterState] {
	toSet' != NotSet and bitfieldIntersection[toSet, setTo.include, toSet']
  }

  pred updateOrSet[toSet: Bitfield + NotSet, setTo: FilterState] {
      (toSet = NotSet and toSet' = setTo.include) or
      (toSet != NotSet and update[toSet, setTo])
  }
```

  </div>
</div>

---

# Putting it Together

We now have a model of what our C++ program is doing: it computes some set of filter flags, then runs a search, excluding the previous flags. It then updates the previous flags with the current search. We can encode
this as follows:

```
fact step {
    always {
        // Model that a new doLookupInScope could've occurred, with any combination of flags.
        all searchState: SearchState {
            some fs: FilterState {
                // This is a possible combination of lookup flags
                possibleState[fs]

                // If a search has been performed before, take the intersection; otherwise,
                // just insert the current filter flags.
                updateOrSet[searchState.previousFilter, fs]
            }
        }
    }
}
```

---
# Are there any bugs?

Model checkers ensure that all properties we want to hold, do hold. To find a counter example, we ask it to prove the negation of what we want.

```C
wontFindNeeded: run {
    all searchState: SearchState {
        eventually some props: Props, fs: FilterState, fsBroken: FilterState {
            // Some search (fs) will cause a transition / modification of the search state...
            configureState[fs]
            updateOrSet[searchState.previousFilter, fs]
            // Such that a later, valid search... (fsBroken)
            configureState[fsBroken]

            // Will allow for a set of properties...
            // ... that are left out of the original search...
            not bitfieldMatchesProperties[searchState.previousFilter, props]
            // ... and out of the current search
            not (bitfieldMatchesProperties[fs.include, props] and not bitfieldMatchesProperties[searchState.previousFilter, props])
            // But would be matched by the broken search...
            bitfieldMatchesProperties[fsBroken.include, props]
            // ... to not be matched by a search with the new state:
            not (bitfieldMatchesProperties[fsBroken.include, props] and not bitfieldOrNotSetMatchesProperties[searchState.previousFilter', props])
        }
    }
}
```

---
# Uh-Oh!

![](./instancefound.png)

---
# The Bug

![bg left width:600px](./bug.png)

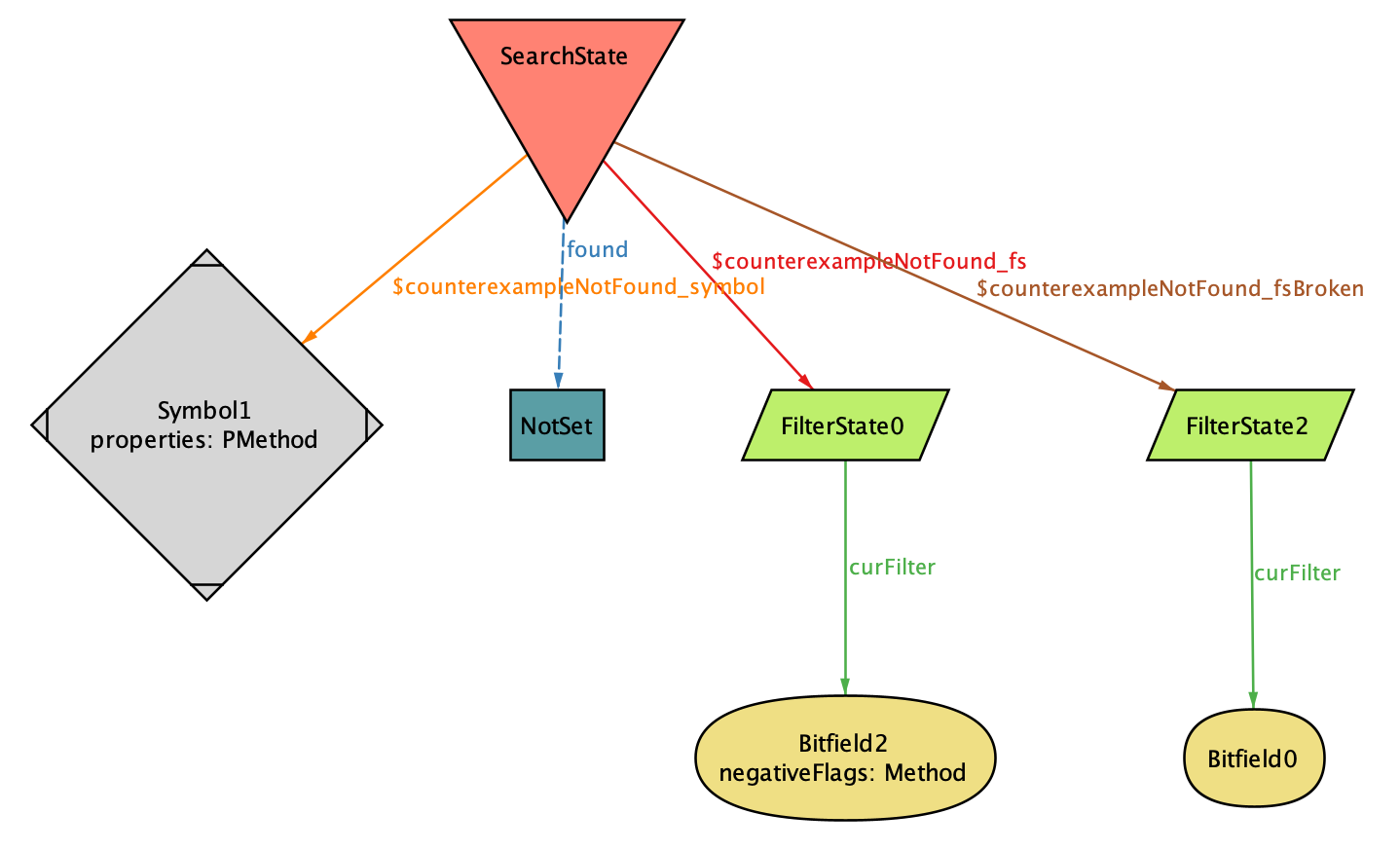
We need some gymnastics to figure out what variables make this model possible.

Alloy has a nice visualizer, but it has a lot of information.

In the interest of time, I found:

* If the compiler searches a scope first for `PUBLIC` symbols, ...
* ...then for `METHOD_OR_FIELD`, ...
* ...then for any symbols, they will miss things!

---
<style scoped>
section {
    font-size: 20px;
}
</style>

# The Reproducer
To trigger this sequence of searches, we needed a lot more gymnastics.

<div class="side-by-side">
  <div>

```chapel
module TopLevel {
  module XContainerUser {
    public use TopLevel.XContainer;
  }
  module XContainer {
    private var x: int;
    record R {}
    module MethodHaver {
      use TopLevel.XContainerUser;
      use TopLevel.XContainer;
      proc R.foo() {
        var y = x;
      }
    }
  }
}
```
  </div>
  <div>

* the scope of `R` is searched with for methods
* The scope of `R`’s parent (`XContainer`) is searched for methods
* The scope of `XContainerUser` is searched for public symbols (via the `use`)
* The scope of `XContainer` is searched with public symbols (via the `public use`)
* The scope of `XContainer` searched for with no filters via the second use; but the stored filter is bad, so the lookup returns early, not finding `x`.

  </div>
</div>